Twistor theory

In theoretical and mathematical physics, twistor theory maps the geometric objects of conventional 3+1 space-time (Minkowski space) into geometric objects in a 4 dimensional space with metric signature (2,2). This space is called twistor space, and its complex valued coordinates are called "twistors."

Twistor theory was first proposed by Roger Penrose in 1967,^[1] as a possible path to a theory of quantum gravity. The twistor approach is especially natural for solving the equations of motion of massless fields of arbitrary spin.

In 2003, Edward Witten^[2] proposed to unite twistor and string theory by embedding the topological B model of string theory in twistor space. His objective was to model certain Yang-Mills amplitudes. The resulting model has come to be known as twistor string theory (read below).

Contents 1 Details 2 Twistor string theory 3 Supertwistors 4 See also 5 Notes 6 Further reading 7 External links

Details

Twistor theory is unique to 4D Minkowski space and the (2,2) metric signature, and does not generalize to other dimensions or metric signatures. At the heart of twistor theory lies the isomorphism between the conformal group Spin(4,2) and SU(2,2), which is the group of unitary transformations of determinant 1 over a four dimensional complex vector space. These transformations leave invariant a Hermitian norm of signature (2,2).

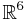• is the real 6D vector space corresponding to the vector representation of Spin(4,2).

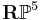• is the real 5D projective representation corresponding to the equivalence class of nonzero points in 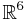under scalar multiplication.

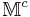• corresponds to the subspace of 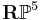corresponding to vectors of zero norm. This is conformally compactified Minkowski space.

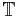• is the 4D complex Weyl spinor representation and is called twistor space. It has an invariant Hermitian sesquilinear norm of signature (2,2).

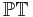• is a 3D complex manifold corresponding to projective twistor space.

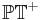• is the subspace of 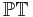corresponding to projective twistors with positive norm (the sign of the norm, but not its absolute value is projectively invariant). This is a 3D complex manifold.

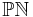• is the subspace of 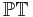consisting of null projective twistors (zero norm). This is a real-complex manifold (i.e., it has 5 real dimensions, with four of the real dimensions having a complex structure making them two complex dimensions).

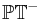• is the subspace of 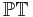of projective twistors with negative norm.

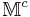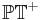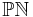, , and 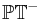are all homogeneous spaces of the conformal group.

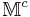admits a conformal metric (i.e., an equivalence class of metric tensors under Weyl rescalings) with signature (+++−). Straight null rays map to straight null rays under a conformal transformation and there is a unique canonical isomorphism between null rays in 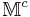and points in 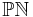respecting the conformal group.

In 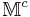, it is the case that positive and negative frequency solutions cannot be locally separated. However, this is possible in twistor space.

Twistor string theory

For many years after Penrose's foundational 1967 paper, twistor theory progressed slowly, in part because of mathematical challenges. Twistor theory also seemed unrelated to ideas in mainstream physics. While twistor theory appeared to say something about quantum gravity, its potential contributions to understanding the other fundamental interactions and particle physics were less obvious.

Witten (2003) proposed a connection between string theory and twistor geometry, called twistor string theory. Witten (2004)^[2] built on this insight to propose a way to do string theory in twistor space, whose dimensionality is necessarily the same as that of 3+1 Minkowski spacetime. Hence twistor string theory is a possible way to eliminate the need for more than 3 spatial dimensions when doing (super)string theory. Although Witten has said that "I think twistor string theory is something that only partly works," his work has given new life to the twistor research program. For example, twistor string theory may simplify calculating scattering amplitudes from Feynman diagrams.

Supertwistors

Witten's twistor string theory is defined on the supertwistor space 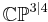. Supertwistors are a supersymmetric extension of twistors introduced by Alan Ferber in 1978.^[3] Along with the standard twistor degrees of freedom, a supertwistor contains N fermionic scalars, where N is the number of supersymmetries. The superconformal algebra can be realized on supertwistor space.

See also

• Penrose transform
• Twistor space
• Invariance mechanics

Notes

Further reading

• Baird, Paul "An Introduction To Twistors"
• Penrose, Roger (1967), "Twistor algebra", Journal of Mathematical Physics 8 (2): 345–366, Bibcode 1967JMP.....8..345P, doi:10.1063/1.1705200, MR0216828, http://link.aip.org/link/JMAPAQ/v8/i2/p345/s1 
• Penrose, Roger (1968), "Twistor quantisation and curved space-time", International Journal of Theoretical Physics (Springer Netherlands) 1: 61–99, Bibcode 1968IJTP....1...61P, doi:10.1007/BF00668831 
• Penrose, Roger (1969), "Solutions of the Zero‐Rest‐Mass Equations", Journal of Mathematical Physics 10 (1): 38–39, Bibcode 1969JMP....10...38P, doi:10.1063/1.1664756, http://link.aip.org/link/JMAPAQ/v10/i1/p38/s1 
• Penrose, Roger (1977), "The twistor programme", Reports on Mathematical Physics 12 (1): 65–76, Bibcode 1977RpMP...12...65P, doi:10.1016/0034-4877(77)90047-7, MR0465032 
• Penrose, Roger (1987) "On the Origins of Twistor Theory" in Gravitation and Geometry, a volume in honour of I. Robinson. Naples: Bibliopolis.
• Penrose, Roger (1999) "The Central Programme of Twistor Theory," Chaos, Solitons and Fractals 10: 581-611.
• Arkani-Hamed, Nima; Cachazo, Freddy; Cheung, Clifford; Kaplan, Jared (2009) "The S-Matrix in Twistor Space."
• Witten, Edward (2003), "Perturbative Gauge Theory As A String Theory In Twistor Space", Communications in Mathematical Physics 252: 189–258, arXiv:hep-th/0312171, Bibcode 2004CMaPh.252..189W, doi:10.1007/s00220-004-1187-3 

External links

• Penrose, Roger (1999) "Einstein's Equation and Twistor Theory: Recent Developments"
• Penrose, Roger; Hadrovich, Fedja. "Twistor Theory."
• Dunajski, Maciej, "Twistor Theory and Differential Equations."
• Hadrovich, Fedja, "Twistor primer."
• Andrew Hodges, "Twistor Theory and the Twistor Programme." Includes many links.
• Huggett, Stephen (2005) "The Elements of Twistor Theory."
• Richard Jozsa (1976) "Applications of Sheaf Cohomology in Twistor Theory."
• Mason, L. J., "The twistor programme and twistor strings:From twistor strings to quantum gravity?"
• Sämann, Christian (2006) "Aspects of Twistor Geometry and Supersymmetric Field Theories within Superstring Theory."
• Sparling, George (1999) "On Time Asymmetry."
• Spradlin, Marcus, "Progress And Prospects In Twistor String Theory."
• MathWorld - Twistors.
• Universe Review "Twistor Theory."
• Twistor newsletter archives

Theories of gravitation Standard Newtonian gravity (NG) General relativity (GR) Introduction History Mathematics Resources Tests post-Newtonian formalism Linearized gravity ADM formalism Historical History of gravitational theory Aristotle's theory Mechanical explanations Fatio–Le Sage Nordström's theory Alternatives to GR Classical theories of gravitation Conformal gravity f(R) gravity Scalar theories Scalar-tensor theories Brans–Dicke Dilaton Self-creation cosmology Bimetric theories Einstein–Cartan Cartan connection Whitehead's theory Nonsymmetric gravitation Scalar-tensor-vector Tensor-vector-scalar Superfluid vacuum theory Logarithmic BEC vacuum Teleparallelism Geometrodynamics Quantum gravity Semiclassical gravity Twistor theory Causal dynamical triangulation Euclidean QG Induced gravity Causal sets Noncommutative geometry Canonical GR Wheeler–DeWitt eqn Loop quantum gravity Superfluid vacuum theory Logarithmic BEC vacuum String theory M-theory Supergravity Superstrings Other Higher-dimensional GR Kaluza–Klein DGP model Gauss-Bonnet gravity Lovelock theory of gravity Lower dimensional gravity 2+1D topological gravity CGHS model RST model Jackiw–Teitelboim gravity Liouville gravity Composite gravity Entropic gravity Massive gravity MOND

Quantum gravity Central concepts graviton · Planck scale · trans-Planckian problem · quantum foam · AdS/CFT correspondence · IR/UV mixing · causal patch · gravitational anomaly · Weinberg–Witten theorem Black holes black hole thermodynamics · black hole information paradox · holographic principle · Bousso's holographic bound · black hole complementarity · gravitational singularity Quantum field theory in curved spacetime Hawking radiation · Unruh radiation · Bunch–Davies vacuum · semiclassical gravity · Casimir effect Proposed theories superstring theory M-theory · supergravity · string field theory · Green-Schwarz mechanism · fuzzball · swampland canonical quantum gravity Wheeler–DeWitt equation · loop quantum gravity Euclidean quantum gravity Hartle–Hawking state superfluid vacuum theory Logarithmic BEC vacuum others noncommutative geometry · causal dynamical triangulation · causal sets · twistor theory Toy models 2+1D topological gravity · CGHS model · RST model · Liouville gravity · type 0 string theory · Jackiw–Teitelboim gravity Applications quantum cosmology eternal inflation · multiverse · FRW/CFT duality Others quantum mechanics of time travel

Works by Roger Penrose Books The Emperor's New Mind (1989) Shadows of the Mind (1994) The Road to Reality (2004) Cycles of Time (2010) Coauthored books The Nature of Space and Time (with Stephen Hawking) (1996) The Large, the Small, and the Human Mind (with Abner Shimony, Nancy Cartwright and Stephen Hawking) (1997) White Mars or, The Mind Set Free (with Brian W. Aldiss (1999) Academic works Techniques of Differential Topology in Relativity (1972) Spinors and Space-Time: Volume 1, Two-Spinor Calculus and Relativistic Fields (with Wolfgang Rindler) (1987) Spinors and Space-Time: Volume 2, Spinor and Twistor Methods in Space-Time Geometry (with Wolfgang Rindler) (1988)